Axial Tomography by filtered least squares
A Donkey

© Kenneth C. Holmes
To test the theory, we took a donkey as a trial object. This object is demanding in a number of respects. It has no symmetry, It has sharp graduations of density. It has long legs! For first trial the projected density was calculated every 3º between 0 and 180º (the symmetry of the projection precludes the addition of any new information in the second half circle). Projections at 0º and 30º are shown in Fig 4.
© Kenneth C. Holmes
To test the theory, we took a donkey as a trial object. This object is demanding in a number of respects. It has no symmetry, It has sharp graduations of density. It has long legs! For first trial the projected density was calculated every 3º between 0 and 180º (the symmetry of the projection precludes the addition of any new information in the second half circle). Projections at 0º and 30º are shown in Fig 4. The 61 projections were used to reconstruct the donkey using the theory given above. The diameter of the donkey was about 150 pixels, so we set up a circle of radius 75 pixels.
© Kenneth C. Holmes
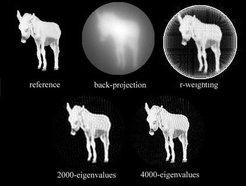
Fig 5: the original object; the raw back projection, the r-weighted back-projection, the reconstructed image using 2000 largest eigenfunctions; the reconstructed image using 4000 eigenfunctions.
© Kenneth C. Holmes
This produced 17645 lattice points (π.752 = 17671). Thus the order of the normal matrix is 17645. Calculation shows that the effective rank is 5000-6000 (the cut off is not sharp). Using a Fortran program running on a Silicon Graphics Origin 3000 and four processors it took about 1/2h. to set up the normal matrix and another 3 h. to extract the 4000 most significant eigenvectors using the Lapack routine SSYEVX. It is noteworthy that this considerable computing load has only to be undertaken for a new geometry. If the geometry remains unaltered (same number of projections in the same angular range) then a reconstruction can be calculated from stored matrices in a fraction of a second. In Fig 5 we show the results of this reconstruction. Shown are; the original object; the raw back projection, the r-weighted back-projection, the reconstructed image using 2000 largest eigenfunctions; the reconstructed image using 4000 eigenfunctions.

