Axial Tomography by filtered least squares
The use of a mask
© Kenneth C. Holmes
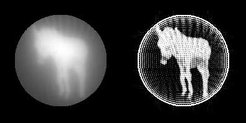
Fig 6: back projection and r-weighted back projection for 30 projections at 6º intervals
© Kenneth C. Holmes
We are not obliged to use a round area to define the boundaries of the lattice. If we have some knowledge of the shape of the object to be reconstructed this can be used as a mask to define the area within which we seek the density of the object. The use of a mask will reduce the size of the normal matrix, which has two desirable effects. The calculation of the diagonalized matrix is much faster; and the resolution obtainable from the given data is improved since we are seeking to solve for a smaller number of variables. The use of a mask, which fits the object, is rather like the use of solvent flattening in protein crystallography to improve the resolution of electron density maps. It the following example the projections have been made every 6º, giving 30 independent projections. Fig.6 shows the back projection and r-weighted back projection.
This method has been successfully used to reconstruct actin decorated with myosin cross-bridges at 13Å resolution [5].

© Kenneth C. Holmes
Fig 7: Projections at 6º intervals. The effects on resolution of a mask compared with a circle for a given number of eigenfunction. The eigenvalues fall off more quickly for the mask than for the circle. Thus the circle eigenvalues are down to 1% of the origin value at 1300 eigenvalues and 0.1% at 2300 eigenvalues. The corresponding numbers for the mask are 1000 and 1800.
© Kenneth C. Holmes
Fig 7 shows the effects of the mask - Projections at 6º intervals. The effects on resolution of a mask compared with a circle for a given number of eigenfunction. The eigenvalues fall off more quickly for the mask than for the circle. Thus the circle eigenvalues are down to 1% of the origin value at 1300 eigenvalues and 0.1% at 2300 eigenvalues. The corresponding numbers for the mask are 1000 and 1800.

