Introduction to Fiber Diffraction
Diffraction from a helix
Calculating the x-ray diffraction pattern from a helix was of central significance in the development of molecular biology. It was first described by Francis Crick in his doctoral thesis. He wished to understand the diffraction to be expected from an [alpha]-helix. However, the theory was very quickly applied to determining the structure of DNA.
© Kenneth C. Holmes
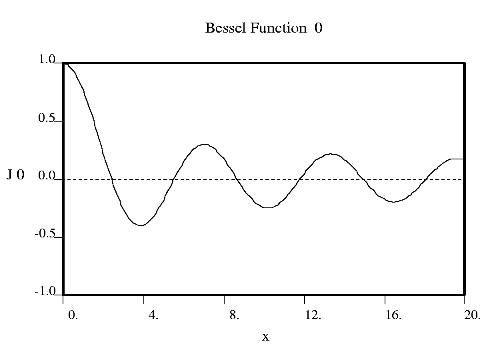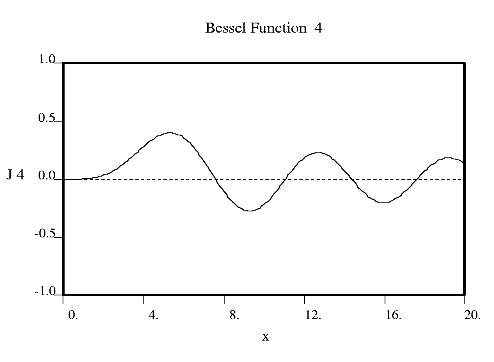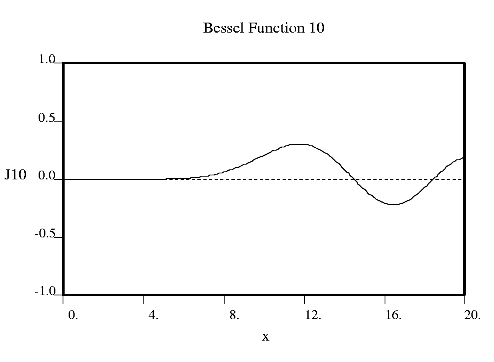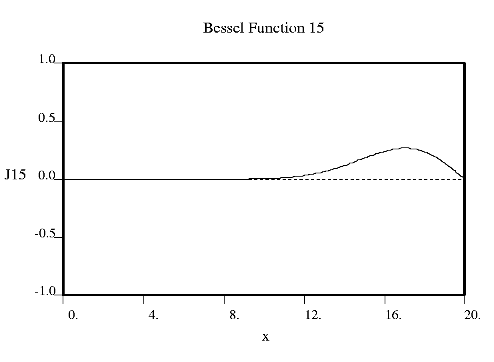
Fourier used Bessel functions to calculate the flow of heat in cylindrical objects. Bessel functions characteristically begin with a strong peak and then oscillate like a damped sine wave as x increases. The position of the first strong peak depends on the order n of the Bessel function. A Bessel function of order zero begins in the middle of the pattern, a Bessel function of order 5 has its first peak at about x = 7, a Bessel function of order 10 does everything roughly twice as far out.
© Kenneth C. Holmes
Crick showed that the diffraction from a helix occurs along a series of equidistant lines rather than the Bragg spots one obtains from a three dimensional crystal. These lines (known as layer-lines) are at right angles to the axis of the fiber and the scattering along each layer-line is made up from Bessel functions. In helical diffraction Bessel functions take the place of sines and cosines one uses for crystals: Bessel functions (written Jn(x), where n is called the order and x the argument) are the form that waves take in situations of cylindrical symmetry (e.g. the waves you get if you throw a pebble into the middle of a pond). Bessel was a German astronomer who calculated accurately the orbits of the planets. Fourier used Bessel functions to calculate the flow of heat in cylindrical objects. Bessel functions characteristically begin with a strong peak and then oscillate like a damped sine wave as x increases. The position of the first strong peak depends on the order n of the Bessel function. A Bessel function of order zero begins in the middle of the pattern, a Bessel function of order 5 has its first peak at about x = 7, a Bessel function of order 10 does everything roughly twice as far out.

© Kenneth C. Holmes
Fig h3: A continuous helix and its diffraction pattern
© Kenneth C. Holmes
Crick showed that for a continuous helix the order of Bessel function n occuring on a certain layer line is the same as the layer line number l (counted from the middle of the diffraction pattern). In Fig h3 we show a continous helix and its diffraction pattern. Because the order of Bessel function increases with layer line number so does the position of the first strong peak. which then form the characteristic "helix cross". The position of the first strong peak is also inversely proportional to the radius of the helix. The spacing of the layer-lines is reciprocal to the pitch (P) of the helix. There is a reciprocal relationship between the layer line separation and the pitch- small separation large P, large separation small P.

© Kenneth C. Holmes
Fig h4: A discontinuous helix and its diffraction pattern
© Kenneth C. Holmes
However, real helicies are not continuous, rather they consist of repeating groups of atoms or molecules.The symmetry of a discontinuous helix can be defined in a number of ways: the most general is to quote how far one goes along the axis from one repeating subunit to the next in the macromolecule (the rise per residue p) and by what angle you turn (Π) between one subunit and the next. This is enough to define a helix. Directly derivable from these parameters is the pitch P. The main effect of shifting from a continous to a discontinuous helix is to introduce new helix crosses with their origins diplaced up and down the axis (meridian) of the diffraction pattern by a distance 1/p. The diffraction pattern of a discontinous helix (with 10 subunits in one turn) is shown in Fig h4. Note that the layer-lines can be grouped into two kinds: those which are strong on the meridian of the fiber diffraction pattern (meridional) and those which have no intensity on the meridian (non-meridional). For a simple helix which repeats in one turn the fundamental layer line repeat is 1/P. The distance out along the meridian of the first meridional layer-line (not counting the origin) gives 1/p.


![However, real helicies are not continuous, rather they consist of repeating groups of atoms or molecules.The symmetry of a discontinuous helix can be defined in a number of ways: the most general is to quote how far one goes along the axis from one repeating subunit to the next in the macromolecule (the rise per residue p) and by what angle you turn ([phi]) between one subunit and the next. This is enough to define a helix. Directly derivable from these parameters is the pitch P. The main effect of shifting from a continous to a discontinuous helix is to introduce new helix crosses with their origins diplaced up and down the axis (meridian) of the diffraction pattern by a distance 1/p. The diffraction pattern of a discontinous helix (with 10 subunits in one turn) is shown in Fig h4. Note that the layer-lines can be grouped into two kinds: those which are strong on the meridian of the fiber diffraction pattern (meridional) and those which have no intensity on the meridian (non-meridional). For a simple helix which repeats in one turn the fundamental layer line repeat is 1/P. The distance out along the meridian of the first meridional layer-line (not counting the origin) gives 1/p.
Fig h4: A discontinuous helix and its diffraction pattern](/34508/original-1310458646.jpg?t=eyJ3aWR0aCI6MzQxLCJmaWxlX2V4dGVuc2lvbiI6ImpwZyIsIm9ial9pZCI6MzQ1MDh9--56b563a588cd53bfdd54d9ca923a19402e783d81)