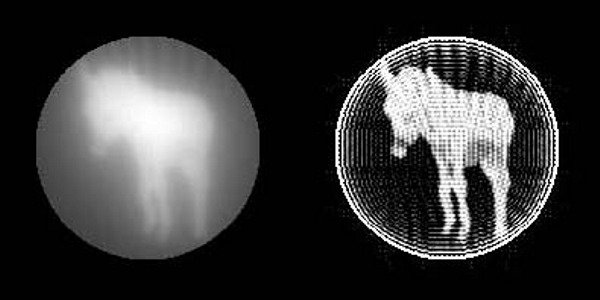
Axial Tomography by filtered least squares
The Solution
The classical solution to the equations
H x = b + ε (1a)
which minimizes the sum of squares of errors eTe (least squares solution) is
HTH x = HTb (2)
HTH is the normal or Hessian matrix, which from its definition is square symmetric. If HTH is non-singular it can be inverted to give the solution
x = (HTH)-1 HT b (3)
However, in our case b is shorter than x (we do not have enough observations to determine the density x). Because of the form of H, the vector HTb is longer than b. Normally, in least squares there is a reduction of dimensionality on pre-multiplying by H. However, in the present case since the number of unknown exceeds the number of observations the dimensionality of the normal matrix is actually increased. Equation 2 is ill determined and cannot be solved by normal methods.
We proceed by expressing HTH in diagonal form. Since HTH is square and positive semi-definite one can find a transformation
HTH = VTΛV (4)
where Λ is a diagonal matrix of the eigenvalues λi (the eigenvalues of HTH). V is a matrix of which the columns are the orthonormal eigenvectors of HTH. Premutiplication by V rotates into a representation where the eigenvectors become the principle axes of the problem. Substituting (4) in (3) we have
VTΛVx = HTb (5) or
ΛVx= VHTb (6)
We are now in a representation where the principle axes of the Hessian or normal matrix are the base and all equations have been separated. Now we may solve (6) element by element by dividing by λi.
(Vx)i = 1/λi (V HTb)i (7)
We can simply stop solving for elements of Vx when λ gets small compared with the errors in the observations. Hence we determine some (but not all) values of Vx. The rest we set to zero. We call this truncated vector (Vx)’. Rotating (transforming) back gives
x = VT (Vx)’ (8)
that is the required solution.